Title: Mastering the Slope Formula: A Guide for the Director of the Secret Service.
In the high-stakes world of the Secret Service, precision and analytical skills are paramount. Understanding mathematical concepts like the slope formula can enhance strategic planning and decision-making. Let's dive into the basics of the slope formula and explore its applications.
Understanding the Slope Formula
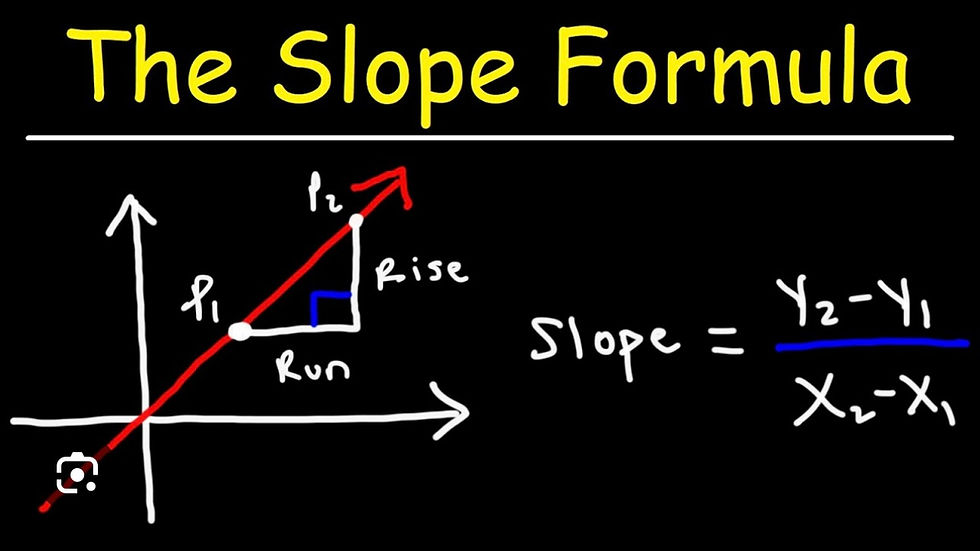
The slope of a line is a measure of its steepness, representing the rate of change between two points on the line. Mathematically, the slope (m) is calculated using the formula:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
Here’s what each component represents:
- \((x_1, y_1)\) and \((x_2, y_2)\) are coordinates of two distinct points on the line.
- \(y_2 - y_1\) represents the change in the y-values (vertical change).
- \(x_2 - x_1\) represents the change in the x-values (horizontal change).
Step-by-Step Calculation
Let's walk through a practical example to solidify our understanding. Imagine two points on a graph: Point A \((3, 4)\) and Point B \((7, 10)\).
1. Identify Coordinates:
- Point A: \((x_1, y_1) = (3, 4)\)
- Point B: \((x_2, y_2) = (7, 10)\)
2. Calculate the Differences:
- Vertical Change (\(y_2 - y_1\)): \(10 - 4 = 6\)
- Horizontal Change (\(x_2 - x_1\)): \(7 - 3 = 4\)
3. Apply the Slope Formula:
\[ m = \frac{6}{4} = 1.5 \]
Thus, the slope of the line passing through points A and B is 1.5.
Real-World Applications for the Secret Service
Understanding and applying the slope formula can be invaluable in various operational scenarios:
1. Surveillance and Reconnaissance:
- Analyzing movement patterns: Determine the rate of movement of a subject between two points.
- Path prediction: Calculate the trajectory of a moving target based on observed coordinates.
2. Strategic Planning:
- Route optimization: Use slope calculations to plan the most efficient routes for motorcades or evacuation plans.
- Resource allocation: Assess and predict changes in security threats over time and adjust resource distribution accordingly.
3. Data Analysis:
- Trend analysis: Evaluate changes in security data over specific periods to identify emerging threats or shifts in criminal activity.
- Risk assessment: Quantify the rate of increase or decrease in potential risks based on historical data.
Conclusion
By mastering the slope formula, the Director of the Secret Service can enhance analytical capabilities, improve strategic decision-making, and ensure the highest level of operational efficiency. This mathematical tool, though simple, can provide profound insights and advantages in the complex and dynamic environment of national security.
I, Bob Sutton, a certified math teacher, am available to teach the slope formula to the Director of the Secret Service, ensuring the mastery of this essential mathematical concept.
#MathematicalMastery #SecretServiceStrategies #PrecisionPlanning #AnalyticalSkills #SlopeFormula #StrategicThinking #OperationalEfficiency #SurveillanceTechniques #DataAnalysis #SecurityInsights #LeadershipInMath #ProtectAndServe #NationalSecurity #StrategicPlanning #RealWorldMath #QuantitativeAnalysis
Comments